2021年6月17日
一次元確率分布からのサンプリングの高速化
こんにちは、LeapMindの徳永です。
確率分布からのサンプリング、してますか?
確率分布からのサンプリングを高速化したいこと、長い人生で、たまにはありますよね。
今回は、低次元(というか、一次元)の連続確率分布からのサンプリングの高速化にチャレンジしてみます。
確率分布からのサンプリングとは?
とりあえず、確率分布という言葉については読者はなんとなく理解しているという前提で話を進めます。
確率分布からのサンプリングとは、ある確率分布に従うサンプルを生成することです。従う、という言葉の意味については一旦見なかったことにして、とりあえず、平均0, 分散1の正規分布から1つ、サンプルを生成してみましょう。以下のスクリプトをPythonで実行してみてください。
import random
print(random.gauss(0, 1))
手元でこのコードを実行してみると、-0.2090941660155127という答えが帰ってきました。しかし、この-0.2090941660155127という値を見ても、これが平均0, 分散1の正規分布から生成されたサンプルなのかどうかはよくわかりません。こういうものは何個もサンプルを取ってこないとわからないものなのです。
試しに、10000個のサンプルを生成して、その平均と分散を調べてみましょう。
import statistics
import random
vals = []
for i in range(0, 10000):
vals.append(random.gauss(0, 1))
print(statistics.mean(vals), statistics.variance(vals))
手元の環境で実行すると次のような結果がかえってきました。
-0.008574148690941068 1.003605854695149
本当に正規分布に従っているのかはこれだけだとよくわかりませんが、ひとまず、平均と分散の値はそれっぽいですね。
様々なサンプリング手法について
サンプリングしたい確率分布がよく知られたものであれば、大抵の場合、効率的なサンプリング手法が確立されているので、それを使えば用は足ります。バグってるかどうかの確認が難しいので、可能な限り自力での実装は避けたほうが無難です。ライブラリを使いましょう。
さて、「自力での実装は避けましょう」と書いたばかりですが、今回は、既存実装の速度に不満がありますので、自力で実装してみたいと思います。どんな確率分布からのサンプリングをしているのかは業務上の秘密に当たるかもしれないので、本稿では例として正規分布からのサンプリングの高速化にトライしてみます。
実は、今回の実装では、確率分布からの厳密なサンプリングは要求されません。そこそこそれっぽく近似できていれば用は足ります。また、確率分布のパラメーターは固定した状態でなんどもサンプリングを行うので、初期化にはかなりの時間をかけても大丈夫です。1秒くらい使ってもまったく問題ありません。
ということで、「厳密じゃなくてもいい」「初期化には時間を使ってもよい」という2点を頭に入れつつ、どういう実装をするかを考えてみます。さらにもう一つ、Pythonで書かれたコードに組み込みたいので、可能であればPythonで書きたい、という制約もつきます。Pythonでループをベタ書きするとscipy等よりも遅くなる可能性が高いので、Ziggurat法みたいなループ回数が事前に決まらない方法は選択肢から外れます。
というわけで、今回は、累積分布関数を区分線形関数で近似して、逆関数法を高速化してみましょう。
逆関数法の区分線形関数による近似
逆関数法の詳しい説明はWikipediaに譲りますが、ある確率分布の累積分布関数の逆関数が計算できれば、その逆関数を使って、一様分布からのサンプリング結果をある確率分布からのサンプリング結果へと変換することができます。
かなり幅広く使える手法ですが、今回の問題設定では、以下のような問題があります。
- ある確率分布の累積分布関数の逆関数をどうやって求めればいいのかわからない。今回の正規分布を例に取ると、そもそも解析的に求められなさそう。
- いい感じに近似できたとしても、それが複雑な形をしていたら、結局、高速化にはつながらない。
複雑な近似を避けて、いくつかの線分で近似しよう、というのが今回の発想です。累積分布関数を区分線形関数で近似してしまいます。こうすれば、複雑な累積分布関数の逆関数を計算する必要がなくなります。
正規分布の累積分布関数をグラフに書くと下図のようになります。
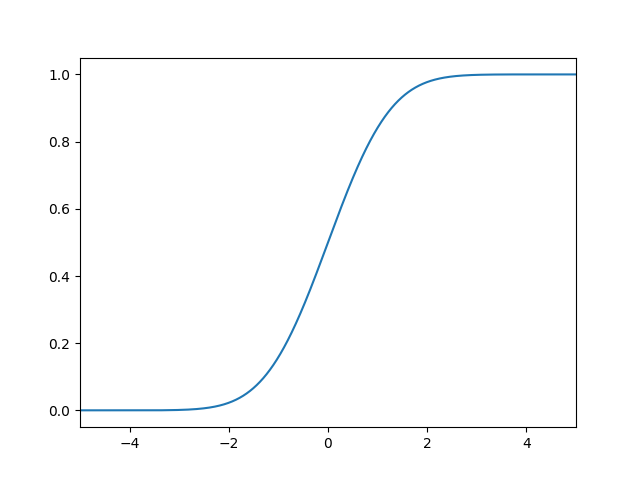
さて、この累積分布関数を、10個の区分線形関数で横方向に輪切りしてみましょう。結果が下図になります。
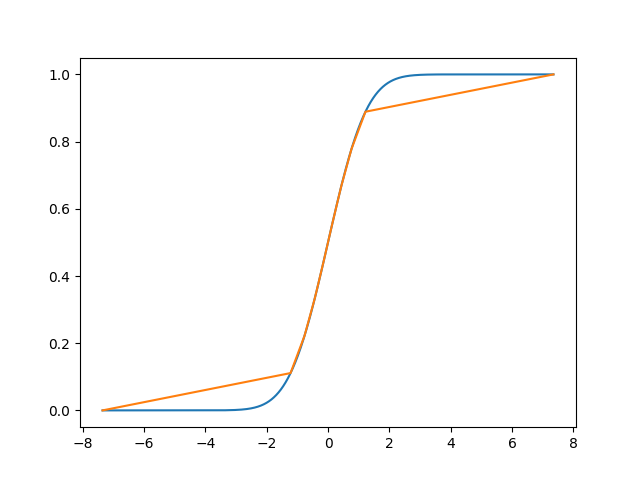
いい感じの図を描くのをサボったので輪切り感が薄いですが、横方向に輪切りにしていると思って心の目でご覧ください。本当は 「一様乱数の平均値を正規乱数として代用する」という話をゆるふわ統計的に検証する - k11i.biz にあるような図が描きたかった…。
さて、10個で近似してしまうと裾の部分が見た目からして明らかにヤバい感じになっておりますが、10000個くらいで近似すると、見た目ではほぼ区別がつかないようになります。
この輪切りされた領域一つ一つをビンと呼ぶことにすると、正規分布からのサンプリングの問題が、ランダムにビンを選択した後、直線のなかの1点をランダムに選ぶ、という問題になります。
これを素直に実装したのが下のコードになります。
import numpy as np
import scipy.stats
class FastGaussianSampler:
def __init__(self, num_bins=8192):
x = np.linspace(1.0e-13, 1.0 - 1e-13, num_bins + 1)
ppf = scipy.stats.norm.ppf(x)
lowers = ppf[0:-1]
uppers = ppf[1:]
self.a = lowers
self.b = uppers - lowers
self.num_bins = num_bins
def generate(self, num):
rands = np.random.randint(0, self.num_bins, size=num)
rands2 = np.random.rand(num)
return self.a[rands] + rands2 * self.b[rands]
動作確認してみる
本当に正規分布らしくサンプリングできているのか、検定をしてみましょう。scipyにはシャピロ・ウィルク検定が実装されているので、標準正規分布であれば簡単に検定できます。検定してみると、手元では以下のような結果が得られました。
ShapiroResult(statistic=0.9980301856994629, pvalue=0.29549142718315125)
P値が0.05より大きければ帰無仮説(=正規分布からサンプリングされている)が棄却されないので、検定を通るくらいには正規分布っぽいと言ってよいでしょう。
ただ、シャピロウィルク検定の中身をしっかり理解できているわけでもないですし、これだけではすこし不安ですね。ねんのためにヒストグラムも描いてみましょう。
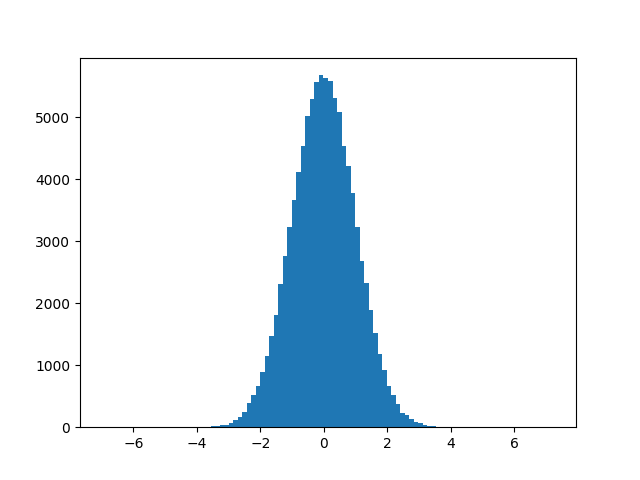
うん、よさそうです。
実験結果
さて、ではお楽しみの速度比較です。どれくらい高速化されたのでしょうか。手元の環境では、65536サンプルを一気に生成してみた場合、以下のような結果になりました。単位は秒です。
ours: 0.0109
scipy: 0.0121
うーん、10%くらいは速くなりましたね。まったく効果がないわけではありませんが、うれしい、と手放しで喜べるほどの結果でもありません。困りました。
GPUを使って高速化してみる
さて、profileを取ってみると、np.random.randintとnp.random.randomの2つで40%ちょっとの時間を使っていることがわかりました。ここの部分は軽い乱数生成器を使えばもっと軽くできそうではありますが、もしここが10倍速くなったとしても、全体としては2倍も速くなりません。
根本的に発想を変えて、GPUを使ってみることにしましょう。今回はPyTorchを使ってみます。
コードの書き換えは機械的に行えます。np.random.randをtorch.randintに置き換えて、np.random.randをtorch.randに置き換えれば大体できあがりです。
GPUを使う都合上、65536サンプルでは速度差がつきづらかったので、サンプル数は1048576個に増やしました。実験してみましょう。結果は以下になります。
ours(cpu): 0.03430
ours(gpu): 0.00142
scipy: 0.04075
元のSciPyでのサンプリングと比較すると、ours(gpu)は28倍くらい速くなっています。これくらい速くなれば、速くなったと言ってもよいでしょう。CPU実装も前の実験と比較するとなんだかパフォーマンスが上がってるっぽい感じですが、これはサーバーでCPUコア数が多いことが原因だと思われます。
GPUを使っているので、パフォーマンス計測に関しては注意する必要があります。今回は、PyTorchでGPUの計算時間を正しく計測する - まったり勉強ノートを参考に、torch.cuda.synchronize()を用いました。
今後の改善点
今回は1つのサンプルを生成するために一様乱数を2つ使っていますが、頑張れば1つでも実装できそうです。(64bit分生成して、上位32bitと下位32bitに分ける、など。疑似乱数の性質がちゃんと保てることを検証しないといけないですが。)今回は元の3〜4倍くらい速くなれば全然ボトルネックにならなくなる(GPU側の計算がボトルネックになる)でこの結果には十分以上に満足しています(ちょっと嘘です、PyTorchのDataLoaderの中でGPUを使うコードを書くとかなり面倒なので、本当はGPUを使わずに済ませたかった。)が、もっとこだわりたいならば、高速化できる余地は残っていると言えそうです。
まとめ
確率分布の累積分布関数を区分線形関数で近似することで、逆関数法をつかったサンプリングを高速化してみました。SciPyの実装と比較して、NumPyでの独自実装は10-20%程度高速化できました。また、PyTorchを使ってGPUで並列化してみたところ、元の28倍くらいの高速化を達成できました。
さて、LeapMindでは確率分布からのサンプリングを高速化したり、それとは全く関係なくいい感じのニューラルネットワークのモデル開発をエンジョイしたりするエンジニアを絶賛募集中です。我こそはと思われる方は以下のURLからどしどし応募してください。